Induced character

In mathematics, an induced character is a character of the induced representation V of a finite group G by W. There is also a notion of induction 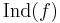$\operatorname{Ind}(f)$ of a class function f on H given by the formula

$\operatorname{Ind}(f)(s) = \frac{1}{|H|} \sum_{t \in G,\ t^{-1} st \in H} f(t^{-1} st).$

However, if f is a character of the representation W of H, then 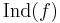$\operatorname{Ind}(f)$ is a character of the induced representation V.^[1]

The basic result is Brauer's theorem on induced characters. It states that a character on G is a linear combination with integer coefficients of characters induced from elementary subgroups.

References

^ Serre, 7.2. Proposition 20.

J.P. Serre, "Linear representations of finite groups". Graduate Texts in Mathematics, vol. 42, Springer-Verlag, New York, Heidelberg, Berlin, 1977,